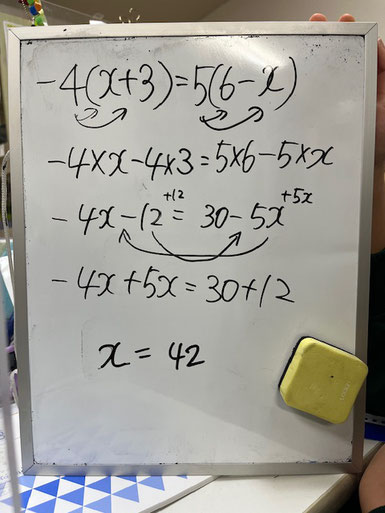

生徒さんのプレゼン内容より
中1数学 文字の計算(分配法則)
こんにちは(-ω-)/
中1の生徒さんがやった
ホワイトボードでのプレゼン内容を
ご紹介したいと思います💁♂️
問題は1次方程式でした。
こちらの生徒さん👧
「移項」の計算でつまづいていて、
「数学がやばい、テストの点数が・・・💧」
と、やばいを強調して
SOS 🚑を出してきました。
テストで何ができなかったか
お聞きすると👂
移項の計算ができない、
とのことでした。
なるほど🤔💭
移項の計算ね。
ボクは移項の計算を教えるときには、
その前段階の「移項の原理」
をお教えします。
移項の原理とは、
なぜ、移項が成り立つのか、
その基本的な考えのことです。
移項というのは、
左辺のプラスが右辺に動くと
マイナスになって、
左辺のマイナスは右辺に行くと、
プラスになるという、
一見すると、不思議な現象です。
そして、けっこう多くの生徒さんが
移項が成り立つ理由を学んで
いながら、
それを忘れていて、
移項の方法だけを覚えているんですね。
😞👋そらあかんで。
この不思議現象がなぜ起こるのかが
わからずにやっていると、
移項の「方法」を忘れたときに、
あえなく撃沈します。
そもそも、不思議なことは
解明しておくべきで、
それこそが勉強ですよね。
Here We Go!💨
さあ、
そこでですが、
まずは、こちらの生徒さんにも
いつも通りに移項の「原理」を
簡単にご説明しました。
簡単に、というのは、
こちらの生徒さんは賢いので、
ある程度は自分で考えて
もらいました。
その方がご本人のためになると
思うからです。
内容の方は、
ここでは省略させていただきます🙇
そして、
なぜ移項が成り立つのかを
理解してもらったのちに、
書いてもらったのが、
このホワイトボードの内容なんです。
こちらのホワイトボードを
お借りしてボクがプレゼンをしてみます
💁♂️
【1行目】
左辺のー4をχと+3の各項に分配をします☝
また、右辺の5を6とーχの各項に
それぞれ分配をします☝
【2行目】
かっこを外すと、こちらのような
式になります☝
【3行目】
計算してまとめるとこのような
式になります☝
そして、左辺のー12を右辺に、
右辺のー5χを左辺に、
それぞれ移項をします☝
移項の計算では、
実際には、
左辺のー12を消すために、
12を両辺に足して、
右辺のー5χを消すために、
両辺に5χを足します。
【4行目】
そうして、できた式がこちらになります。
見かけ上は、
左辺のー12は、
右辺に行くと+12に変わり
右辺のー5χは、
左辺に行って+5χになっています。
これで移項の完成です。
【5行目】
この式を計算して、
答えは42となります。
生徒さんにプレゼンしてもらい
ましたが、
しっかりとできていました
👏👏👏
ホワイトボードも実にうまく
まとまっていると
思います。
移項計算、また分配法則にも
不安があったようですが、
プレゼンをやってみて
プラス+
問題演習をして、
完全に理解して計算も
できるようになりました。
さらに、もう一度、やってもらった
内容が、
もうひとつのホワイトボード
(2枚目の方)です。
「学校の先生が書いたの❓」
と思えるような
ポイントをしっかりと押さえて
書かれていると思います🤗
大したもんだと思います👏
というわけで、
移項というのは、
なぜその移項とやらが成立するのか、
その理由(原理)を理解して
おく必要があって、
そのうえで、それらを意識して
問題を解く必要があると
思います。
基本が大事なんですね。🤔
🌸最近のブログ
ホームページ👈プッシュ
部活と勉強の両立について👈プッシュ
プレゼンテーション授業の解説について2👈プッシュ
プレゼンテーション授業の解説について1👈プッシュ
英語の教科書の音読②👈プッシュ
英語の教科書の音読①👈プッシュ
やる人、やらない人、3つのパターン👈プッシュ
同じ問題が出たのになぜできない?👈プッシュ
やっているのになぜできない?👈プッシュ
やっているのになぜできない?2👈プッシュ

コメントをお書きください