

公式を使うときには、
なぜそういう公式になるのかを
考えることが大事。🤔💭
こんにちは(-ω-)/
小5の算数の授業では、
図形の面積についての
内容をやっているようです。
ひし形の面積を求める問題でも
公式があります。
こちらでもやりました。
【ひし形の面積】
ひし形の面積=対角線×対角線÷2
対角線同士をかけて2で割る。
(2つの対角線はそれぞれ違う対角線)
ワークの問題で、
ちょっとひねった問題で、
ひし形のまわりを長方形で囲んであって、
それをヒントに
面積を求める問題がありました。
こちらの生徒さんは、しっかりと正解する
ことができました👏
ここでですが、なぜ、対角線×対角線÷2が
ひし形の面積の公式になるのかを
聞いてみました。👂
すると、それについては
わかりませんでした。
むしろ、そんな質問をされて
「意外🤔❓」
というような顔をしていましたね。
公式は知ってはいるが、
その公式が示す意味までは
考えていなかったのです。
どんな図形であっても、
公式を使って計算ができることは
大事ですが、
その公式の示す意味を考えることも
大事です。
面積を求めることはできるが、
算数や数学といった教科は、
ただ計算ができればいいというものでは
ありません。
ただ計算をするのであれば、
公式を知らなくても、
それを調べて
その公式にあてはめて計算すればいいだけの
話しで、だれにでもできます。
そして、それ以上のものはありません。
公式が示すものがなんなのか❓
これを考えることがとても重要と
僕は考えています。
なので、この手の問題が出てきた
ときには、同時に
「なぜその公式になるのか❓」
と生徒さんに質問するように
しています。
✋ただしですが、
円の面積(半径×半径×3.14)や
中1での球体の体積や表面積といった
公式については(👆参照)
これまでの知識で解くことは
まず不可能なので、
それはそれで、そのまま公式を覚えて
「公式を使いこなす問題」として
割り切って進めます。
なので、可能な限り、
その公式がどうやって導かれたのかを
考えていただきます。
1.その公式の意味を知って、
その公式を使いこなす☝
2.公式を使いこなす。
公式に関する問題は、2つの道(2Way)
があると理解しています。
先ほどの生徒さんですが、
公式の意味を知って、
まるで「感動」したような表情をして
いました。
決して、大げさな表現ではありません👋
「全米も泣いた」❓
これは大げさです(笑)
全米を泣かせるようにとは言っていますが(笑)
このように、なぜそうなのかを知ることは、
勉強に対しての興味関心を引くという
意味でも、とてもいいことだと思います。
中3の展開・因数分解の公式、
二次方程式の解の公式など、
これらも、それまでに習った知識で、
導き出すことができるものです。
そもそも、わけのわからないまま
公式を使っているよりも、
その意味、理由を知って、
問題を解く方が健全であると
僕は考えます🤔💭
なぜその公式になるのか❓
例をあげて説明します。

今年(2024-25年)の高校志願者状況には
「異変」が生じているようです。
昨年度は、私立の人気が上がりましたが、
今年は、公立の人気がかなり
高いようです。
「物価高」の影響でしょうか?
入試の倍率が上がるのかは、
ふたを開けてみたいとわからない
ものですが、
今年の場合は、
学校見学でも公立高は例年より
かなりにぎわっているようです。
いったいどうなることやら。。。
さて、引き続いて、公式に関する
内容のお話です。
公式をしっかりと覚えていないのに
問題を解こうとする生徒さんも
多いんです。
(>_<)
公式を使わないと解けない問題を
公式を覚えていないで、
解けるのでしょうか❓
公式は覚えていたつもりでも、
うる覚え程度では、
いずれ忘れてしまいます。
公式は、
まずはしっかりと覚えこむ。
そして、問題を解いて実際に使って
覚える、
そうお伝えしています。
そこで、その公式ですが、
その公式がどうやって生まれたのかを
知らないで、
疑問すら持たずに使っている
というのはどうなんでしょうか❓
数学や算数の授業では、
その公式がどうやって生まれたのかを
習うはずです。
ただし、
球の表面積や体積のような
高校で習う知識がないとわからない
ようなヤツは、
とりあえず公式は「丸覚え」しか
ありません。
さて、今回は、その公式が
どうやって生まれたのかを、
例をあげてお話をします。
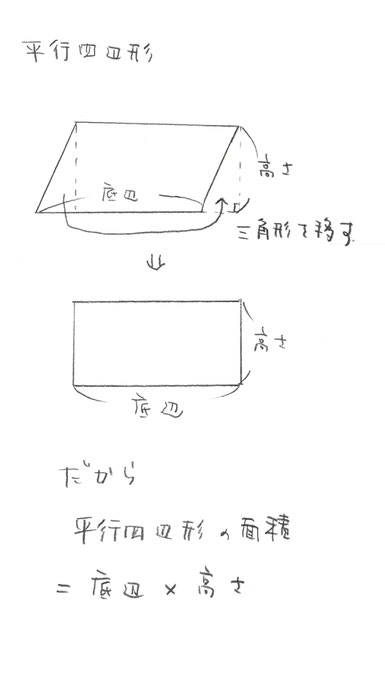
上図の平行四辺形について、
平行四辺形の面積の公式は
面積=底辺×高さ です。
その公式がなぜそうなるのかが
わからないのなら、
そこで、立ち止まって
「なぜ❓」と考えることが大事だと
思います。
なぜなのかというと・・・
図の通り、平行四辺形の左端の
三角形をたてに垂直に切り取って、
反対側にくっつけてしまうと、
長方形ができます。
この長方形の横の長さは、
平行四辺形の底辺の長さと
同じになります。
また平方四辺形の高さは、
長方形のたての長さにあたります。
よって、
この平方四辺形の面積
=この長方形の面積
となって、
長方形の面積が
たて×横 なので、
たて×横=この平方四辺形の面積
となります。
ここでの、たて×横は底辺×高さと
同じなので、
平方四辺形の面積
=たて×よこ=底辺×高さ
となります。
次いで、三角形の面積です。
三角形の面積は、底辺×高さ÷2です。
なぜ、底辺×高さ÷2なのか❓
なぜ÷2なのか❓
こんな疑問をもってほしいですね。
上の図において、
三角形を頂点から底辺に垂線を
引いて、三角形を2つにわけます。
①の三角形と、②の三角形ができあがります🤗
この三角形をちょうど囲い込むように
長方形で囲ってみます。
そうすると、長方形の中に①の三角形と、
②の三角形が2つずづできます。
この長方形の面積は
三角形の底辺(よこ)×高さ(たて)
と同じになります。
長方形のたて×よこが、
三角形の底辺×高さと
同じになります。
たて×よこ=底辺×高さ
で、
三角形の実際の面積は、
①と②の三角形1個分ずつの和(足し算)で、
長方形の中には、
①と②の三角形が2個分ずつあるので、
「÷2」をする必要があります。
考え方は一通りではないのですが、
こんな感じでなぜそうなるのかを
とらえておく必要があると思います。
算数が苦手な人は、
こういった内容については
わかってないことがほとんどです。
またそして、
「算数が得意」と自分で言っていても、
なぜそうなるのかについて
関心がない、という方は、
本当の意味で算数が得意とはいえないと
思います。
それくらい「なぜ❓❓❓」を考えることは
基本的で大事だと思うのです。
🏠当塾のホームページ👈push
ブログを更新しています。
🌸その他のブログ
(以下の各項目をpushすると、blogに飛びます💁♂️)
💁♂️「定義」と「定理」をわかりやすく説明します。中2数学
💁♂️「定義」と「定理」をわかりやすく説明します。part2 中2数学
💁♂️まちがえやすい式の約分 中1数学 めちゃくちゃくわしい例題解説
💁♂️英語のストレスを軽減する方法。
💁♂️間違えやすい符号の扱い。中1数学
💁♂️絶対値がわからない? 中1数学
💁♂️関連単語・熟語を一網打尽。英語
💁♂️💁♂️💁♂️

コメントをお書きください